309BIR: Session 12

• Combining different investments can achieve more than just a simple spreading of risk.
• Appropriately selected combinations can actually reduce the level of risk without affecting the expected return.
• It is this that makes portfolio construction such a powerful investment strategy.
• The key to unlocking this strategy is an understanding of the correlation between assets
  

---

• When the price of A goes up, the price of B goes down: we can say that the daily returns of A and B are negatively correlated.

---

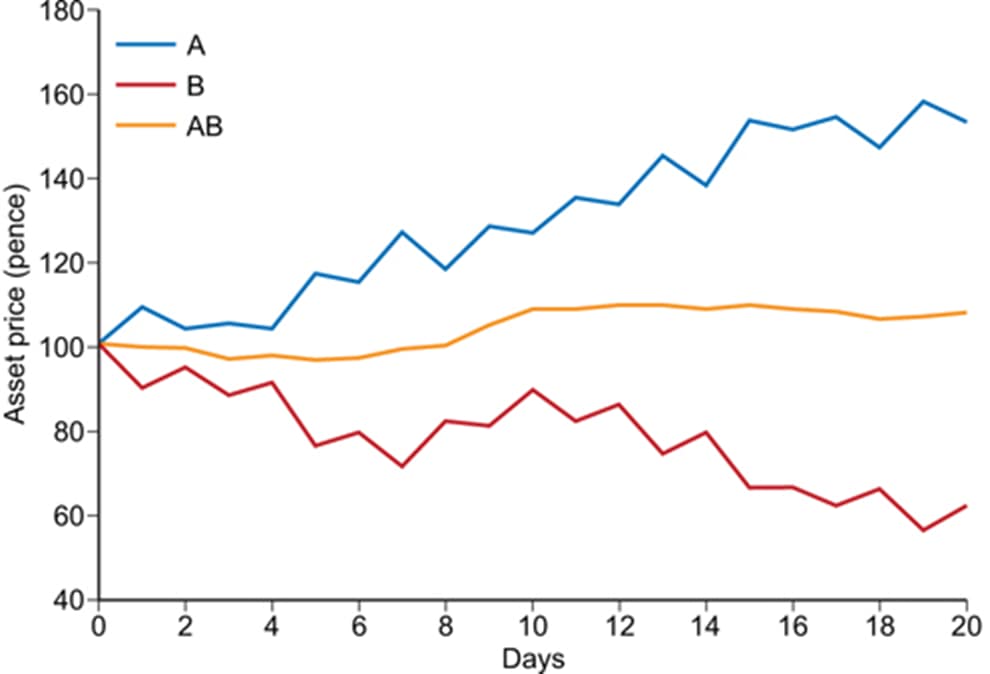
• If we combine the two assets A and B (50 per cent of our portfolio in each) we get the line AB:
  • instead of ups and downs across the period, the combination of the two risky assets results in a nice smooth line.
• The smoothness of the line indicates a low risk of price movements either up or down although, as the risk is reduced, so is the return relative to holding just A.

• Investors might opt for AB if they are risk averse and give higher priority to avoiding short-term fluctuations than to seeking the highest possible return over the whole investment term.
• This would imply that investors view the systematic negative correlation of the daily returns of A and B as stronger and more likely to persist than either the overall upward trend of A or the downward trend of B.

• The exact correlation is measured by the ‘correlation coefficient’,
  essentially an index number that records the degree to which two series of values (in this case, daily returns) vary (or not) in line with each other.
• The correlation coefficient lies between −1 (perfectly negative correlation) and 1 (perfectly positive correlation).

• A correlation of −1 means that all points of the scatter plot are found on a straight line with a decreasing slope.
  • It tells us that as the values for Asset A rise, values for Asset B would fall, and vice versa.
• A correlation of 1 is the exact opposite: all points would be on a straight line with a positive slope.
  • It tells us that Asset A and Asset B would rise and fall together.
• A correlation of 0 means that there is no particular linear association between the two series.

(Excel->Option->Adds-in-> “Analysis ToolPak” and click “Ok”/Go to spreadsheet with prepared data->Data Analysis->Correlation->Extract R in another sheet)

---

Using correlation in practice

• You have seen what correlation means and there were hints above about how it could be used to smooth returns from financial assets, indicating opportunities for risk reduction.
• In particular, a negative correlation between the returns of two assets is highly desirable.
• However, although combining negatively correlated assets can smooth out ups and downs in day-to-day performance, it does not necessarily produce large cumulative returns over the full investment term.
• So, it is important to think about what we want to correlate and over which period.
• For example, take two assets whose prices go in the opposite direction every day but on average are on a downward trend month after month:
  • the combination of the two would give a smooth pattern of the average daily value of the portfolio but this value would be decreasing over several months
  • this means a negative correlation between their daily returns and a positive correlation between their monthly returns (that is both are negative each month).
• Moreover, the correlation coefficient, whatever the period of returns used to calculate it, is always based on past data:
  • past trends may not be repeated and so can be a poor predictor of future outcomes.

---

• As long as the investor is aware of these limitations, the correlation remains a very useful tool to identify opportunities for risk diversification.
• Combined with fundamental analysis, it can guide the asset allocation strategy of the investor in creating portfolios that target a desired level of return with no more than the level of risk the investor can tolerate.

• Unlike the expected return, the risk of the portfolio is not simply the weighted average of the risk of its components.
• We need to take into account the correlation between these components.
• This is at the core of modern portfolio theory, derived by Harry Markowitz in the mid-twentieth century.

Portfolio rebalancing sounds boring, but it’s a powerful investment strategy

https://www.cnbc.com/2015/10/21/portfolio-rebalancing-sounds-boring-but-its-a-powerful-investment-strategy.html

Risk of a two-share portfolio



• Unlike the expected return, the risk of the portfolio is not simply the weighted average of the risk of its components.
• We need to take into account the correlation between these components.
• This is at the core of modern portfolio theory, derived by Harry Markowitz in the mid-twentieth century.

---

The risk of the two-share portfolio is equal to the sum of three terms:

• the risk of the first asset in the portfolio, weighted by its proportion in the fund

• the risk of the second asset in the portfolio, also weighted by its proportion in the fund
• a term that includes the correlation coefficient.
  • Remember:
    • the more negative the correlation coefficient, the more the reduction of total risk, thanks to this third term that reduces the weighted sum of individual risks (that is, the first two terms).
    • At the other extreme, when the correlation coefficient is equal to 1, no reduction in risk is possible.

---

• Provided correlation is less than perfect, the benefit of diversification even when assets are positively correlated is good news for the real world.
• As you have seen, the total risk of an asset includes the systematic risk of the market in which it is traded and so this asset is likely to be at least partially positively correlated with other assets evolving in the same market.
• These findings of the modern portfolio theory have been at the core of asset allocation strategies over the last fifty years.

---

• As the price of shares varies over the full, say, five or ten-year period so does the proportion of their value in the portfolio if their number is kept constant.
• The direct implication of this is that the risk of some types of portfolios has increased the term of the investment, due to the larger proportion of riskier shares.

---

Portfolio Rebalancing

• The alternative strategy, consistent with the principles of modern portfolio theory is to keep the proportion of the value of the portfolio invested in each of the shares constant.
• This can be called diversification by value.
• This portfolio implies that the investor must review the portfolio at the end of each period (e.g. each month).
• As the prices of the shares change, the investor will have to sell some of any shares that have increased in value and buy more of any shares that have fallen in value, in order to keep constant the relative contribution of each to the value of the portfolio.

---

• This ‘value’ strategy is implicit in Markowitz’s diversification, for each holding period.
• It also lies behind the investment management strategy of rebalancing –
  • in other words, periodically, selling some assets and buying others to restore the original asset allocation by value and,
  • hence, the original level of risk.
• The implications of the two strategies – volume or value – for the returns of the portfolio may be quite different.

---

• Note that in practice the real-world investment strategy of rebalancing will typically be somewhere in between a pure value and pure volume approach because:
  • Transaction costs and taxation of capital gains reduce the benefits from rebalancing very frequently.
  • Overtrading may also increase total market volatility and instability.

---

• To maintain constant value proportions in your portfolio, the rebalancing strategy implies selling assets which have increased in value and buying more assets whose value has decreased (a ‘sell high/buy low’ strategy).
• Some would argue that this is a sensible strategy although in practice many investors actually do the opposite (keep the winners and sell the losers).
• These behaviours are highly related to the way investors consider how markets work.

https://www.youtube.com/watch?v=DW0HNMeuZVo

https://hbr.org/1982/01/does-the-capital-asset-pricing-model-work

• In practice, building an efficient portfolio is quite time-consuming and may be costly,
  because one needs to assess the characteristics of each share in the market and each possible portfolio to establish where the efficient frontier lies.
• In real markets, there may be many thousands of combinations.
• Provided one accepts some assumptions, the Capital Asset Pricing Model (CAPM) offers both a simpler way to build an efficient portfolio and superior combinations of risk and return.

• If we add a further assumption that all investors are looking at the same risk-return spectrum, this implies that if all investors have optimized their portfolio, then the only combination of shares they can hold is that which exists in the market:
  • after having bought and sold different assets to each other, they have reached an equilibrium which represents the best combination possible and is located on the efficient frontier.
• Now the only way they can obtain a different combination of risk and return is to combine the market portfolio with a risk-free asset in different proportions,
  suitable to their risk attitude/tolerance.

---

• Two more assumptions are needed in order to make this strategy possible (and simple to explain):
  • the risk-free asset is risk-free for everyone, and
  • investors can borrow and lend at the same risk-free rate.

---

The Capital Asset Pricing Model

• When you increase the proportion of market securities in the portfolio, you increase the level of risk; hence you expect the investor to be rewarded with a higher return.
• Conversely, when the proportion of M is decreased, the investor gets a less risky portfolio.
• Depending on their attitude to risk, each investor can find the portfolio that suits them best.

• Note that one could also borrow at the risk-free rate in order to increase further the number of market securities one can hold.
• If you move the slider beyond 100 per cent of market securities, you allow for the possibility that the investor is negative in cash (they borrow) in order to overload their portfolio P with the market index and reach risk-return combinations that are superior to the efficient frontier.

---

Measuring performance

• Strict followers of the CAPM would be passive investors,
  • in other words, they would hold a single fund representing the market portfolio and
  • combine this with a risk-free asset (say, cash or government bonds) to achieve the mix of risk and return they want.
• The market portfolio can also serve as a benchmark to evaluate strategies pursued by active investors.
  • different funds can be built with a diverse mix of risky assets in order to try to beat the market (the benchmark).

---

• Some managers believe that they have superior skills or information available to them,
  • or that markets are not efficient,
  • allowing for prices to be predictable to some extent,
  • so that there could be opportunities to secure higher returns for a given level of systematic risk
    • just by changing the composition of the portfolio.

---

Remember the two main types of active investing:

• changing the amount of cash (buying and selling M) depending on how the market behaves
  • (market timing exercise);
• overloading the risky portfolio with more attractive shares (deviating from M), which are expected to perform better than the benchmark
  • (stock selection/picking exercise).

More

Portfolio Theory and the Capital Asset Pricing Model (page: 198)

https://bibliu.com/app/?query=%22the%20Capital%20Asset%20Pricing%20Model%22#/view/books/9781260568356/epub/OEBPS/chapter8.html#page_205

• One way to consider these active strategies is to use a simple indicator that would depend on the correlation between a particular asset and the chosen benchmark – in this case, the market portfolio.
• By definition, the asset must be one of the many constituents of the market portfolio.
• So the correlation would, in effect be a measure of the contribution that this specific asset makes to the risk and return of the portfolio as a whole.
• It is called the beta (or alternatively the beta coefficient).

---

• Beta is a more powerful measure because it also informs us about the magnitude of the relationship.
• Beta is a measure of the volatility of an asset relative to its market.
• It is a measure of the extent to which the asset’s return goes up and down with the market as a whole.

• A beta of 1 tells us that the return from the asset changes exactly in line with the market as a whole.
• The market portfolio itself must by definition have a beta of 1.
• A tracker fund – in other words, a portfolio which tries to replicate the market risk and return – would be expected to have a beta close to 1.
• A positive beta of less than 1 indicates that the asset moves with the market but not by as much.
• A beta of more than 1 indicates an asset that moves more strongly than the market both when the market is rising and when it is falling.

---

Interpreting beta

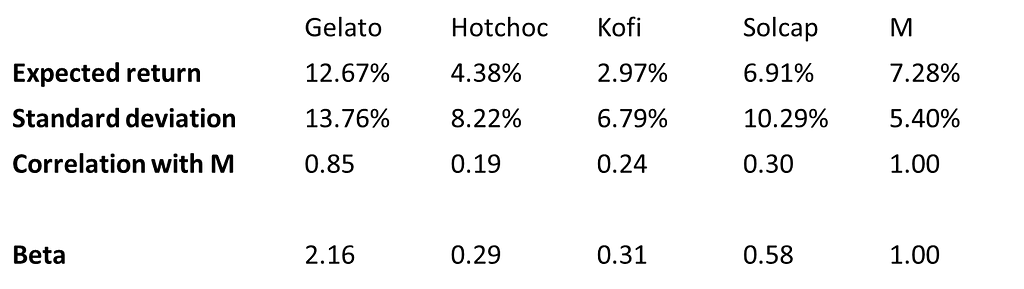
• Let’s look at the betas of some imaginary shares, with the benchmark being the portfolio Koblanc as our representation of the market portfolio.
• On the next slide, you can see the Betas of the four shares of interest, Gelato, Hotchoc, Kofi and Solcap, (reproduced in Table 4.1 below).

---

Activity

1. Gelato has a beta of nearly 2.2. What does this mean?
2. Compare it to the beta of Hotchoc.
3. Looking at the betas of Kofi and Hotchoc, would you say these are low-risk shares?

---

Calculating the beta of a portfolio

• An advantage of beta is that it is easy to compute. Moreover, if it is well measured (the reference should be the relevant market as a whole), we can also use individual betas to compute the beta of any portfolio.
• When we know the individual betas of the components of a portfolio, the beta of the portfolio is simply the weighted average of the betas of its components.
• For example, the portfolio Kocap is made up of 64 per cent shares in Kofi and 36 per cent shares in Solcap.
• Therefore:
  • Beta of Kocap = 64% × beta of Kofi + 36% × beta of Solcap
  • = 64% × 0.31 + 36% × 0.58 = 0.40

You have learnt:

• that, investors who follow the CAPM tend to adopt a passive strategy:
• they invest in funds that mimic the market portfolio and a risk-free asset in proportions depending on their personal risk attitude
• in practice, investors do not all behave as the CAPM would suggest. Some adopt a different strategy – a more active
• that the performance of the investment portfolios created by investors can be assessed using various performance measures, which take into account not only the amount of return but also the risk involved in their strategies.

• CII (2012) Financial Services, Regulation and Ethics R01. Diploma in Regulated Financial Planning study text, London: The Chartered Insurance Institute.
• CII (2014) Investment Planning AF4. Advanced Diploma in Regulated Financial Planning Study Text, London: The Chartered Insurance Institute.
• Rutherford, J. (2010) Risk-Return Strategies in Mazzucato, M., Lowe, J., Shipman, A. & Trigg, A. (eds) (2010) Personal Investment: Financial Planning in an Uncertain World Basingstoke: Palgrave Macmillan / The Open University.
• Open University, Online Unit 3: Unpacking Portfolio Construction [online], https://learn2.open.ac.uk/mod/oucontent/view.php?id=238980 (Accessed 22 August 2013).
• YouTube (2009) Interview with Harry Markowitz, [online], http://www.youtube.com/watch?v=5Y1MBc_Vj3w&feature=fvw (Accessed 22 Jan 2014).